DDOSvoid's Blog

2021牛客多校1 I Increasing Subsequence

发表于 分类于
本文字数： 2.5k 阅读时长 ≈ 2 分钟

题目描述

https://ac.nowcoder.com/acm/contest/11166/I

Solution

首先我们发现可以通过算概率得出期望

我们令 $f[i][j]$ 表示第一个人走到 $i$，第二个人走到 $j$ 的且当前轮到第一个人走

$g[i][j]$ 表示第一个人走到 $i$，第二个人走到 $j$ 的且当前轮到第二个人走

我们发现所求的期望就是 $\sum f[i][j]+g[i][j]$

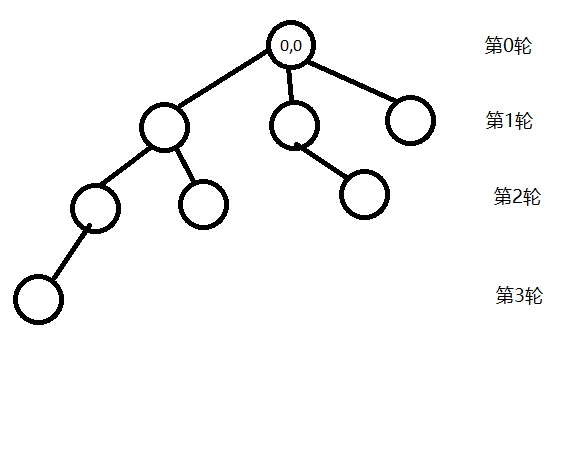
至于原因，我们可以这样考虑，首先我们记录的 $f[i][j]$ 实际上是第一轮走到 $(i,j)$ 的概率加上第二轮走到 $(i,j)$ 的概率加上第三轮$\cdots$

然后我们考虑一下如果记录轮数的实际转移的样子

无标题.png

我们在叶子计算概率乘上深度等价于在每个点计算一次概率，注意到一个节点的值等于所有儿子节点的值的和

原因在于这个点在向下转移的时候是将自己的权值拆成若干份(概率和相加为 $1$)乘下去的

那么我们现在就得到了一个 $O(n^3)$ 的 $dp$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
f[0][0] = 1;
for (int i = 0; i <= n; ++i)
    for (int j = 0; j <= n; ++j) {
        if (f[i][j]) {
            int cnt = 0; 
            for (int k = i + 1; k <= n; ++k)
                if (a[k] > max(a[i], a[j])) ++cnt;
            for (int k = i + 1; k <= n; ++k)
                if (a[k] > max(a[i], a[j])) g[k][j] = (g[k][j] + f[i][j] * inv[cnt]) % p;
        }
        if (g[i][j]) {
            int cnt = 0; 
            for (int k = j + 1; k <= n; ++k)
                if (a[k] > max(a[i], a[j])) ++cnt;
            for (int k = j + 1; k <= n; ++k)
                if (a[k] > max(a[i], a[j])) f[i][k] = (f[i][k] + g[i][j] * inv[cnt]) % p;
        }
    }

然后我们考虑如何优化，我们发现 $f[i][j]$ 在转移的时候，$j$ 是不动的且只会转移到大于 $i$ 的一些 $k$

那么我们考虑做一个前缀和的优化，我们改变 $dp$ 数组的含义

我们令 $f[i][j]$ 表示第一个人要选一个大于 $i$ 的位置，第二个人当前在 $j$，现在轮到第一个人选，$g[i][j]$ 同理

那么当 $a[i+1]>a[j]$ 时，我们可以将 $f[i][j]$ 转移到 $g[i+1][j]$，同时 $f[i][j]$ 也要转移到 $f[i+1][j]$，$g[i][j]$ 的转移同理

不过这时候我们要注意统计答案时要统计能正确转移的答案，$cnt$ 和逆元可以预处理

时间复杂度 $O(n^2)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <iostream>
#include <vector>
#define maxn 5010
#define ll long long
#define INF 1000000000
using namespace std;

const int p = 998244353;

ll pow_mod(ll x, ll n) {
    ll s = 1;
    for (; n; n >>= 1, x = x * x % p)
        if (n & 1) s = s * x % p;
    return s;
}

ll inv[maxn];

int n, a[maxn], cnt[maxn][maxn];

ll f[maxn][maxn], g[maxn][maxn];

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr); cout.tie(nullptr);

    cin >> n;
    for (int i = 1; i <= n; ++i) cin >> a[i];
    for (int i = n; i; --i)
        for (int j = 0; j <= n; ++j) cnt[i][j] = cnt[i + 1][j] + (a[i] > j);
    inv[1] = 1; for (int i = 2; i <= n; ++i) inv[i] = -(p / i) * inv[p % i] % p;
    f[0][0] = 1; ll ans = 0; 
    for (int i = 0; i <= n; ++i)
        for (int j = 0; j <= n; ++j) {
            if (f[i][j] && i < n) {
                if (a[i + 1] > a[j]) {
                    g[i + 1][j] = (g[i + 1][j] + f[i][j] * inv[cnt[i + 1][a[j]]]) % p;
                    ans = (ans + f[i][j] * inv[cnt[i + 1][a[j]]]) % p;
                    f[i + 1][j] = (f[i + 1][j] + f[i][j] * (cnt[i + 1][a[j]] - 1) % p * inv[cnt[i + 1][a[j]]]) % p;
                } else f[i + 1][j] = (f[i + 1][j] + f[i][j]) % p;
            }
            if (g[i][j] && j < n) {
                if (a[j + 1] > a[i]) {
                    f[i][j + 1] = (f[i][j + 1] + g[i][j] * inv[cnt[j + 1][a[i]]]) % p;
                    ans = (ans + g[i][j] * inv[cnt[j + 1][a[i]]]) % p;
                    g[i][j + 1] = (g[i][j + 1] + g[i][j] * (cnt[j + 1][a[i]] - 1) % p * inv[cnt[j + 1][a[i]]]) % p;
                } else g[i][j + 1] = (g[i][j + 1] + g[i][j]) % p;
            }
        }
    cout << (ans + p) % p << "\n";
    return 0;
}